[DP] BOJ 2579번 문제풀이
문제 분석
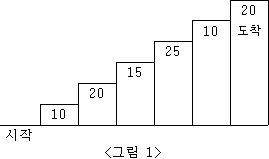
각 계단을 오를 때 계단에 적혀있는 숫자의 합이
가장 큰 경우를 구하는 문제다.
조건은 다음과 같습니다.
- 계단은 한 번에 한 계단씩 또는 두 계단씩 오를 수 있다. 즉, 한 계단을 밟으면서 이어서 다음 계단이나, 다음 다음 계단으로 오를 수 있다.
- 연속된 세 개의 계단을 모두 밟아서는 안 된다. 단, 시작점은 계단에 포함되지 않는다.
- 마지막 도착 계단은 반드시 밟아야 한다.
자, 지금부터
s[i] = 계단의 적힌 숫자
d[i][j] = 현재까지 j 개의 계단을 연속해서 밟고, i 번째 계단에
올라섰을 때의 점수 합의 최댓값이라고 합시다.
(단, i 번째 계단은 반드시 밟는다.)
이상태에서 주어진 계단에 대해서 한번 값을 찾아봅시다.
첫 번째 계단에서는 이러한 값이 도출됩니다.
d[1][1] = s[1] , d[1][2] = 0
d[1][1] 은 자명하게 s[1] 이라는 것을 알 수 있습니다.
또한, d[1][2] 은 불가능하기 때문에 d[1][2] = 0 으로 둡시다.
※ 현재 설명은 이해를 돕기위해 1-indexed 기반의 설명을 하지만, 코드는
0-indexed 기반으로 되있습니다.
두 번째 계단에서는
d[2][1] = s[2], d[2][2] = s[1] + s[2]
d[2][1] 은 두 번째 계단까지 한 개의 계단을 밟았다는 의미이므로 첫 번째 계단을
안 밟았다는 의미가 된다.
반대로 d[2][2] 는 두 개의 계단을 밟았기 때문에 첫 번째, 두 번째 계단을 모두
밟았다는 의미가 된다.
세 번째 계단에서는
d[3][1] = max( d[1][1], d[1][2]) ) + s[3]
d[3][2] = d[2][1] + s[3]
d[3][1] 부터는 경우의 수가 나뉜다. 계단을 한번 연속적으로 밟았기 때문에
직전 계단인 s[2] 을 밟지 않았다는 의미가 된다.
그러면 d[1][1] 와 d[1][2] 두 가지의 경우의 수가 나뉘고 그중
최댓값에 마지막 계단을 더해주면 된다.
d[3][2] 같은 경우는 무조건 이전 계단인 s[2]를 밟았으며
이미 연속적으로 2번을 밟은 상태이므로 d[2][1]의 경우만
존재한다.
여기까지 이해하셨다면 반드시
계단그림을 그려보고
경우의 수를 따져보시길 바랍니다. (꼭)
이제 점화식이 감이 오나요?
d[i][1] = max( d[i-2][1], d[i-2][2] ) + s[i]
d[i][2] = d[i-1][1] + s[i]
이러한 점화식이 나왔다면 처음에
상수값으로 도출되는 초깃값을 정의해주시고
코드를 짜 보신다면
답을 맞히실 수 있을 겁니다.
코드
#include "bits/stdc++.h"
using namespace std;
int d[301][2];
int n;
int s[301];
int main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cin >> n;
for (int i = 0; i < n; i++)
{
cin >> s[i];
}
d[0][0] = s[0];
d[0][1] = 0;
d[1][0] = s[1];
d[1][1] = s[0] + s[1];
for (int i = 2; i < n; i++)
{
d[i][0] = max(d[i - 2][0], d[i - 2][1]) + s[i];
d[i][1] = d[i - 1][0] + s[i];
}
cout << max(d[n - 1][0], d[n - 1][1]);
}