[알고리즘] 집합 찾기(Union Find)

List

---

1. 연결 리스트를 이용한 집합 찾기
2. 배열을 이용한 집합 찾기
3. 트리를 이용한 집합 찾기
4. 연산의 효율을 높이는 법
    ※ 코드구현은 생략

 

연결 리스트를 이용한 집합 찾기

---

 연결리스트를 이용한 표현에서 집합의 원소는 노드로 표현이 됩니다. 각 노드에는 원소를 저장하는 필드, 다음 원소와 대표 원소를 기리키는 두 개의 포인터가 있습니다. 다음 원소를 가리키는 포인터를 통해 집합의 모든 원소들이 연결됩니다. 여기서 대표 원소는 각 집합의 가장 앞에 있는 원소를 의미합니다. 그리고 각 집합에는 마지막 원소를 가리키는 tail 변수 라는것이 존재합니다. 이 변수는 두 집합을 합칠 때 이용됩니다.

 

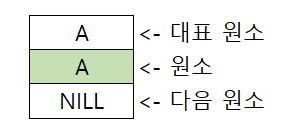
 하나의 원소 x 만을 갖고 있는 집합이 있다고 가정해봅시다. 연결 리스트의 한 노드의 구성은 오른쪽 이미지와 같을 것입니다. 집합의 원소가 하나이기 때문에 대표 원소는 자기 자신이 될 것입니다. 원소 필드에는 x가 입력되고, 다음 노드는 없으니 포인터 값은 NILL로 설정됩니다.

 

 

 노드가 하나 있을 때도 역시 집합이라 표현할 수 있습니다. 이제 두 개의 집합을 합치는 과정을 살펴봅시다. 아래의 그림을 보시면 A 를 대표 원소로 갖는 집합과 D 를 대표 원소로 갖는 집합이 있습니다. 두 개의 집합을 합치려고 할 때, 원소의 수가 적은 집합을 원소의 수가 많은 집합에 붙이는 게 좋을까요??? 아니면 원소의 수가 많은 집합을 적은 집합에 붙이는 것이 좋을까요??? 당연히 큰 집합을 그대로 유지한 상태에서 작은 집합을 붙이는 것이 효율적입니다. 왜냐하면 어떠한 집합 하나를 다른 집합에 연결하기 위해서는 모든 원소의 대표 원소 포인터를 변경해주어야 하기 때문이죠. 이런 방식으로 두 집합을 합치는 것을 무게를 고려한 합집합(Weighted Union) 이라고 합니다.

 

 

 

 

 

배열을 이용한 집합 찾기

---

배열은 연결 리스트와 굉장히 유사합니다. 구현의 차이만 있을 뿐입니다.  우선 대표 원소와 다음 원소를 가리키는 포인터 변수 두 개와 데이터를 저장할 변수 하나를 갖는 CLASS를 만들어 줍니다. 그리고 이 CLASS를 변수로 갖는 배열을 선언하면 완성됩니다. 역시 모양은 연결 리스트와 같고 배열에 값을 넣어보면 아래 그림과 같이 될 것입니다.

 

배열을 합치는 방법도 연결 리스트에서 하는 것과 같고 역시 구현에서만 차이가 생깁니다. 연결 리스트는 사이즈를 조절해줄 필요가 없지만 배열은 Resize 작업을 계속해주어야 한다는 점!!. 이 부분만 주의하시면 문제없으리라 생각합니다.

 

 

 

 

 

트리를 이용한 집합 찾기

---

트리를 이용하면 연결 리스트보다 효율적인 방법으로 처리가 가능합니다. 각 집합을 하나의 트리로 표현하는 방법인데, 기존의 배운 트리 방식과는 조금 다른 방식을 사용합니다. 보통 트리의 노드를 구현할 때, 부모 노드가 자식 노드를 가리킵니다. 하지만 집합 표현에서는 자식 노드가 부모 노드를 가리키는 방식을 사용합니다. 이렇게 하면 임의의 노드에서 부모 노드를 계속해서 추적하다 보면 무조건 루트 노드를 만나게 됩니다. 감이 오시나요?. 트리에서 루트 노드는 대표 원소를 의미하게 됩니다. 따라서 루트 노드의 부모 노드 역시 자기 자신인 루트 노드가 됩니다. 이런 식으로 트리를 구현해보면 아래의 그림과 같이 구현이 가능합니다.

 

 

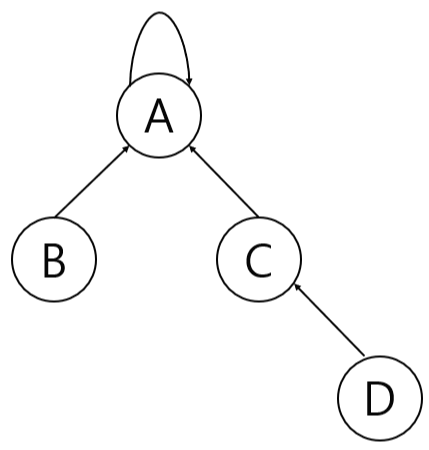
배열과 연결 리스트를 이용한 집합의 합집합에서는 무게를 고려한 합집합 방식을 사용하였습니다. 이는 모든 노드의 대표 원소 포인터를 바꿔주어야 하기 때문이었습니다. 하지만 트리는 대표 원소를 루트 노드로 공유하고 있기 때문에 루트 노드의 부모 노드만 바꾸어 주면 되기 때문에 무게를 고려할 필요가 없습니다. 따라서 원하는 집합에 원하는 집합을 붙이면 되겠습니다. 

합쳐서 대표가 되는 집합을 주집합, 합쳐지는 집합을 부집합이라고 해보겠습니다. 그림에서는 부집합의 대표 원소 포인터를 주집합의 대표 노드로 해주었습니다. 하지만 트리의 특성상 부집합의 대표 원소 포인터를 주집합의 어떤 노드로 해주어도 두 집합은 합쳐집니다. 왜냐? 아까 말했다시피 부모 노드를 계속해서 추적하다 보면 나오는 루트 노드가 그 집합의 대표 노드가 되기 때문이죠.

 

 

 

연산의 효율을 높이는 방법

---

1. 랭크(Rank)를 이용한 Union

 이 방법을 이용한 트리의 각 노드는 자기 자신을 루트로 하는 서브 트리의 깊이를 랭크(Rank)라는 이름으로 저장합니다. 그러면 집합의 대표 노드의 랭크 값이 가장 클 것이고 밑으로 내려갈수록 1씩 줄어드는 그림이 될 것입니다. 

 갑자기 랭크를 이용하는 이유는 역시 무게를 고려한 합집합(Weighted Union) 방식을 사용하기 위해서입니다. 트리는 합치는 과정에서 소요되는 시간이 언제나 같습니다. 하지만 합친 후의 탐색 시간을 고려한다면?  분명 달라질 겁니다. 그래서 랭크를 최소화하기 위해 높은 랭크를 주집합, 상대적으로 낮은 랭크를 부집합으로 Union 을 하게 됩니다. 이 경우 랭크가 같은 집합을 Union 하지 않는 이상 랭크가 높아지는 일은 없습니다. ex)  주집합(Rank 2) + 부집합(Rank 2) = 집합(Rank 3)

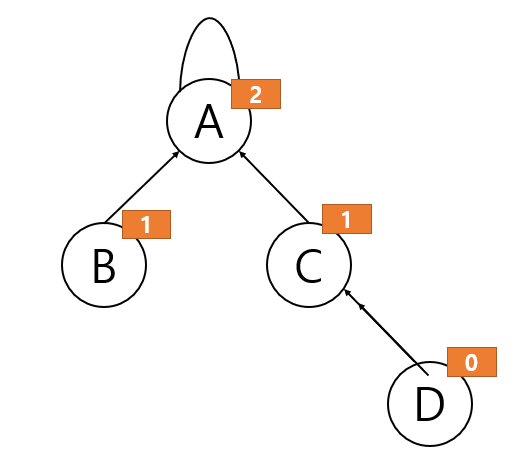
Rank 를 적용한 집합 트리

 

 

2. 경로 압축

 경로 압축 방법은 말 그대로 트리의 깊이를 줄이는 방법입니다. 임의의 노드를 탐색하는 경로에 놓인 모든 노드의 부모 노드를 대표 노드로 바꾸는 것입니다. 이렇게 하면 대부분의 경우 트리의 깊이를 줄여서 탐색 효율을 높일 수 있을 것입니다. 여기서 제가 모든 경우라고 말하지 않은 경우는 아주 소수의 경우가 있기 때문입니다. 예를 들어 랭크가 1인 집합에서는 이 방법을 사용해도 바뀌는 것이 없기 때문에 깊이가 줄어들지 않습니다. 또한, 이미 루트 노드를 부모 노드로 가리키는 노드를 탐색하는 경우에는 경로 압축이 되지 않습니다. 

 

출처 : https://bowbowbow.tistory.com/26