[알고리즘] 동적 계획법(Dynamic Programming)

List

---

1. 동적 계획법(Dynamic Programming) 이란?
2. 피보나치수열 구현
3. 메모이제이션(memoization)

 

동적 계획법(Dynamic Programming)

---

 이 알고리즘은 다이나믹 프로그래밍 또는 DP라고 많이 불립니다. 이전에 배웠던 알고리즘과 차이가 있다면 큐(queue) , 스택(stack)처럼 특정 자료구조를 사용해야 하는 고정적인 개념이 아니라는 겁니다. 이름의 프로그래밍(Programming) 이란 단어가 의미하는 것은 컴퓨터 언어로 코딩을 하는 것을 말하는 것이 아니라 "계획하다"의 의미를 갖고 있습니다.  따라서 이 알고리즘은 특정 문제들을 특수한 형태로 계획해서 풀어나가야 할 때 사용됩니다.

 

 동적 계획법은 대회나 SW 역량테스트 등의 등장 빈도가 아주 높고 기본 소양으로 취급되는 분야이기 때문에 문제의 수도 굉장히 많습니다. 그렇기 때문에 이 알고리즘을 잘 사용할 수 만 있다면 풀 수 있는 문제들이 상당히 많아집니다. 지금부터 동적 계획법이 무엇인지 살펴봅시다.

 

우선 동적 계획법을 사전 검색하면 이렇게 나옵니다.

동적 계획법(動的計劃法, dynamic programming)이란 복잡한 문제를 간단한 여러 개의 문제로 나누어 푸는 방법을 말한다. 이것은 부분 문제 반복과 최적 부분 구조를 가지고 있는 알고리즘을 일반적인 방법에 비해 더욱 적은 시간 내에 풀 때 사용한다.

 

문제를 여러 개로 나누어 푸는 방법에는 분할 정복이 있죠. 하지만 분할 정복과 DP는 결정적인 차이가 있습니다. 분할 정복은 분할했을 경우 반복적인 문제가 발생하지 않습니다. 하지만 DP는 반복적인 문제가 발생하기 때문에 메모이제이션(Memoization)기법들이 필요하게 됩니다. 또한 이 과정에서 DP는 별도의 메모리를 소비하기 때문에 그리디 알고리즘에 비해 시간 복잡도는 크지만 문제를 풀 수 있는 스펙트럼이 넓고 근삿값이 아닌 최적의 값을 얻을 수 있습니다.

 

이해를 돕기 위해 절취선 아래에 예시를 준비했습니다.

 

---

 

동적 계획법을 입문하는데 가장 많이 사용하는 개념 중 하나가 피보나치 수열(Fibonacci numbers) 입니다.

 

피보나치 수열 점화식

 

피보나치수열은 아시다시피 0번째 와 1번째의 값은 특정되고

2번째부터는 이전 두항의 값의 합으로 결정됩니다.

 

코딩의 재귀 함수를 배울 때 역시 많이 보게 되는데

코드로 간단하게 구현하면 아래와 같습니다.

 

#include <iostream>
using namespace std;
 
int fibonacci(int n){
    if(n == 0) return 0;
    if(n == 1) return 1;
    return fibonacci(n-2) + fibonacci(n-1);
    //피보나치 함수 안에서 다시 피보나치 함수를
    //재귀적으로 부르는 형태이다.
}
 
int main(){
    int N;
    cin >> N;
    cout << fibonacci(N) << endl;  
}

 

피보나치 함수의 내부를 보면 0 과 1인 경우는 0 과 1을 

바로 return 해줍니다.

 

그 외에 경우에는 이전 두 개의 피보나치를 재귀적으로 불러옵니다.

이때, N이 한자리의 정수 정도일 경우에는 큰 문제없이 프로그램이 돌아갑니다.

 

하지만 30 ~ 40 정도만 넘어가도 웬만한 컴퓨터에서 값이 바로 출력되지 않을 겁니다.

30 ~ 40 정도의 숫자가 엄청 큰 숫자도 아닌데도 불구하고

실행시간이 오래 걸리는 이유를 한번 살펴봅시다.

 

 

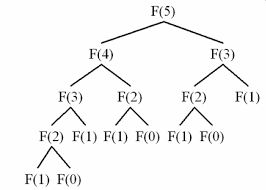
위에 보이는 트리는 5번째 피보나치수열을 구하기 위한 과정을 보여줍니다.

이 과정은 지금 코드로 구현되어 있는 재귀 함수의 과정과 일치합니다.

 

처음에 F(5) 의 이전 두개 항인 F(4) 와 F(3) 을 구하기 위해 피보나치 함수를

재귀 호출 합니다. F(3) 을 먼저 구한다면 다시 F(1) 과 F(2) 를 재귀 호출합니다.

그런데 여기서 F(2) 의 값을 얻기 위해 F(1) 과 F(0) 을 다시 호출합니다.

심지어 !!! 

F(4) 를 구하기 위한 모든 과정에서 이미 구했던 값은 다 잊어버리고 

처음부터 다시 재귀 호출을 통해 구하는 것을 볼 수 있습니다.

 

이런 식으로 이미 구했던 값을 반복적으로 다시 구하는 과정 때문에

호출 횟수는 기하급수적으로 늘어나게 됩니다. 

이렇게 되면 상수 시간을 벗어나 지수 시간의 시간 복잡도가 발생합니다.

이것은 피보나치수열의 일반식을 통해 증명이 가능합니다.

 

그렇다면 이러한 문제를 피하기 위해서는 어떠한 방법을 

사용하면 좋을까요?

 

이런 경우 사용하는 것이 바로 메모이제이션(Memoization) 기법입니다.

말 그대로 제가 앞에서 구한 값들을 저장해두는 것이죠.

 

 

#include <iostream>
#include <vector>
using namespace std;
 
vector<int> dp;
 
int fibonacci(int n){
    if(n == 0) return 0;
    if(n == 1) return 1;
    if(dp[n] != -1) return dp[n];
    //이미 구했다면 바로 리턴
    dp[n] = fibonacci(n-2) + fibonacci(n-1);
    return dp[n];
}
 
int main(){
    int N;
    cin >> N;
    dp.resize(N+1, -1); // 초기값 -1은 절대 나올 수 없는 값
    cout << fibonacci(N) << endl;
}

 

이 코드를 보면 dp라는 벡터가 추가되었습니다.

이건 배열로 해도 문제는 없습니다.

하지만 resize 와 초기화가 간편한 벡터를 추천드립니다.

 

그리고 함수 내부를 보시면 함숫값을 출력 전에 dp에 저장을 하는 과정이 있습니다.

이 부분이 바로 메모이제이션 기법을 사용한 부분입니다.

 

이렇게 구하는 모든 값들을 배열에 저장해두었다가 이미 구한 값을 

사용해야 하는 경우에 계산과정을 생략하고 바로 출력할 수 있도록 만든 것입니다.

 

이렇게 되면 한번 계산한 값은 다시 구할 필요가 없기 때문에 O(N)의 상수 시간이 소요됩니다.

하지만 이 기법을 사용하면 별도의 메모리를 사용해야 하는 단점이 있습니다.

고급 동적 계획법을 배우게 되신다면 메모리를 사용하지 않는 방법도 있습니다.

 

 

< 예시 문제 + 풀이 >

---

 

2019/05/04 - [프로그래밍/1일1백준] - [DP] 1463번 문제풀이

[DP] 1463번 문제풀이

2019/05/04 - [프로그래밍/1일1백준] - [DP] BOJ 2579번 문제풀이

[DP] BOJ 2579번 문제풀이

2019/05/06 - [프로그래밍/1일1백준] - [DP] BOJ 1149 번 문제 풀이

[DP] BOJ 1149 번 문제 풀이

2019/05/11 - [프로그래밍/1일1백준] - [DP] BOJ 11726 번 문제

[DP] BOJ 11726 번 문제

2019/05/11 - [프로그래밍/1일1백준] - [DP] BOJ 1912 번 문제풀이

[DP] BOJ 1912 번 문제풀이

2019/05/13 - [프로그래밍/1일1백준] - [DP] BOJ 11053 번 문제 풀이

[DP] BOJ 11053 번 문제 풀이